MATERI SBMPTN FISIKA Mekanika

---

Hubungan Gerak Lurus dan Melingkar

---

Gerak Lurus	Gerak Melingkar
s = jarak	θ = sudut jarak
v = kecepatan	ω = kecepatan sudut
a = percepatan	α = percepatan sudut

Hubungannya:
s = θR
v = ωR
a = αR
Keterangan:
R : Jari-jari lingkaran (m)

---

Gerak Parabola

---

Rumus Parabola pada sumbu-X (GLB)

1. v_tx = v_0x = v₀ cos α
2. x = (v₀ cos α)t

Keterangan:
v_0x : Kecepatan awal pada sumbu-X ( m/s)
v_tx : Kecepatan sesaat pad a sumbu-X ( m/s)
x : Jarak pada sumbu-X saat waktu t (m)

Pada saat jangkauan maksimum

1. x_maks = [(v₀)² sin 2α] / g
2. t_{x maks} = [2v₀ sin 2α] / g

Rumus Parabola pada sumbu-Y (GLBB)

1. v_0y = v₀ sin α
2. v_ty =V₀ sin α - gt
3. h = (v₀ sin α)t - (1/2)gt²

Keterangan:
v_0y : Kecepatan awal pada sumbu-Y (m/s)
v_ty : Kecepatan sesaat pada sumbu-Y(m/s)
h : Ketinggian saat waktu t (m)
g : Percepatan gravitasi (10 m/s²)

Pada saat ketinggian maksimum:

1. t_{h maks} = (v₀ sin α) / g
2. h_maks = [(v₀)² sin² α] / 2g

---

Gerak Vertikal Ke Atas

---

Cirinya memiliki kecepatan awal (v₀)
Ketinggian maksimum yang dicapai:
h_maks = (v₀)² / 2g

Waktu tempuh untuk mencapai ketinggian maksimum:
t_maks = v₀ / g

---

Gerak Jatuh Bebas

---

Cirinya tanpa kecepatan awal (v₀).
Waktu yang dibutuhkan benda ketika menyentuh tanah:


Kecepatan benda jatuh bebas ketika menyentuh tanah:

---

Konsep Gaya

---

a. Gaya Berat (w)

Gaya berat arahnya selalu ke bawah, dan besarnya adalah:
w=mg
Keterangan:
w : Berat benda (N)
m : Massa benda (kg)
g : Percepatan gravitasi (m/s2)

b. Gaya Normal (N)

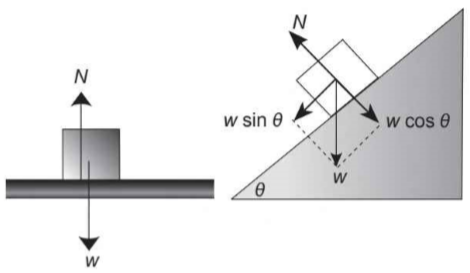
Arah GAYA NORMAL selalu TEGAK LURUS terhadap BIDANG SENTUH.
Gaya ini tidak memiliki rumus yang pasti, disesuaikan dengan gaya yang bekerja pada benda tersebut. Untuk menentukan gaya normal, gunakan hukum I Newton.

c. Gaya Gesek (f)
Arah gaya gesek selalu berlawanan arah dengan kecenderungan gerakan. Ada dua keadaan yang terjadi pada benda, yaitu:

1. Benda TETAP DIAM
   Benda akan TETAP DIAM, jika gaya F yang kita berikan masih KURANG atau SAMA DENGAN GAYA GESEK STATIS MAKSIMUMNYA (fs_maks).
   F ≤ fs_maks
   F ≤ μ_sN
   Jadi, besarnya gaya gesek (f) adalah sama dengan gaya yang yang diberikan pada benda, yaitu F.
   f= F
2. Benda BERGERAK
   Benda akan BERGERAK, jika gaya F yang diberikan bemilai LEBIH BESAR dari gaya GAYA GESEK STATIS MAKSIMUMNYA (fs_maks)
   F > fs_maks
   F > μ_sNJadi, besarnya gaya gesek (f} pada benda adalah gaya gesek kinetis, rumusnya:
   f = f_k = µ_kN
   
   Keterangan:
   f : gaya gesek (N)
   fs_maks : gaya gesek statis maksimum (N)
   f_k : gaya gesek kinetis (N)
   µ_s : koefisien gesekan statis
   µ_k : koefisien gesekan kinetis
   N : gaya normal (N)

---

Hukum Newton tentang Gerak

---

a. Hukum I Newton

∑F = 0

Rumus ini digunakan untuk 2 keadaan, yaitu benda diam (seimbang statis) dan benda bergerak lurus beraturan/GLB (seimbang dinamis).

b. Hukum II Newton

∑F = ma

Rumus ini digunakan untuk kondisi benda bergerak lurus berubah beraturan (GLBB).

c. Hukum lll Newton
F_aksi = -F_reaksi
Keterangan:
∑F : Resultan gaya (N)
m : Massa (kg)
a : Percepatan (m/s²)

---

Gerak Lurus

---

a. Gerak Lurus Beraturan {GLB)
Syarat:
KECEPATAN TETAP atau PERCEPATANNYA NOL (v = tetap atau a = 0).
Rumus jarak
s = vt
Keterangan:
s : Jarak (m)
v : Kecepatan (m/s)
t : Waktu (s)

b. Gerak Lurus Berubah Beraturan {GLBB)
Syarat:
KECEPATAN BERUBAH atau PERCEPATANNYATETAP (v = berubah atau a = tetap).
Rumus-rumus GLBB:

1.  s = v₀t + (1/2)at²
2.  v_t =V₀ +at
3.  (v_t)² = (v₀)² + 2as
4.  s = [(v_t + v₀) / 2] . t

Keterangan:
s : Jarak (m)
a : Percepatan (m/s²)
v_t : Kecepatan sesaat pada waktu t (m/s)
v₀ : Kecepatan awal (m/s)
t : Waktu (s)

---

Gerak Lurus

---

a. Gerak Melingkar Beraturan {GMB)

Syarat:
KECEPATAN SUDUT TETAP (ω) atau PERCEPATAN SUDUTNYA NOL (α)
(ω = tetap dan α = 0).
Rumus GMB:
θ=ω.t
Keterangan:
θ : Jarak sudut (rad)
ω : Kecepatan sudut (rad/s)

b. Gerak Melingkar Berubah Beraturan {GMBB)
Syarat:
KECEPATAN SUDUT BERUBAH-UBAH atau PERCEPATAN SUDUTnya TETAP.
(α = tetap)
Rumus-rumus GMBB

1. θ = ω₀.t + (1/2).α.t²
2. ω_t = ω₀ + α.t
3. (ω_t)² = (ω₀)² + 2.α.θ
4. θ = [(ω_t + ω₀)/2] . t

Keterangan:
θ : Jarak sudut (rad)
ω₀ : Kecepatan sudut awal (rad/s)
ω_t : Kecepatan sudut sesaat (rad/s)
α : Percepatan sudut (rad/s²) ]
t : Waktu (s)