Bagian 1
-
x3 - x2 + 5x + 1
x3 - x2 + 2x + 4
x3 - x2 + 4x + 2
x3 - x2 + x + 5
x3 - x2 + 3x + 3
Jawaban : e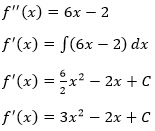
garis singgung y = f(x) di titik A(1,6) mempunyai gradien 4, berarti f' (1) = 4

Grafik y = f(x) melalui titik A(1,6), berarti f(1) = 6
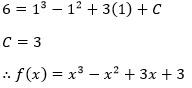
-
1/9√3
1/9√2
1/6√3
1/6√2
1/3√2
Jawaban : ePerhatikan gambar berikut.
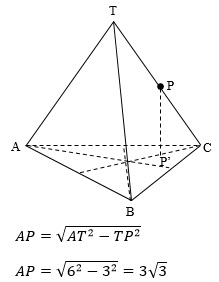
Perhatikan segitiga ABC
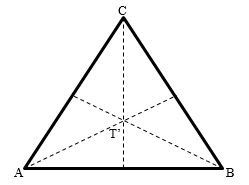
Berdasarkan aturan pada segitiga samasisi AT' = 2/3 AP
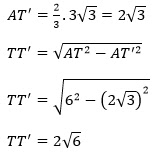
Kemudian berdasarkan prinsip kesebangunan
PP' = ½ . 2√6 =
Perhatikan segitiga APP'

-
 Jawaban : e
Jawaban : e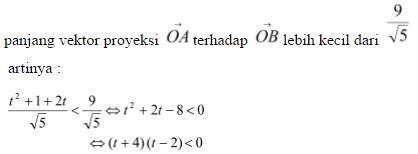
Sehingga:
-4 < t < 2
-
Jawaban : a
* P(x) = (x2– x – 2) Q(x) + (x + 2) maka
P(2) = (x2– x – 2) Q(2) + (2 + 2) = 4
P(– 1) = (x2– x – 2) Q(– 1) + (– 1 + 2) = 1
** Q(x) dibagi (x + 2) mempunyai sisa 3 maka Q(–2) = 3
P(– 2) = ((– 2)2– (– 2) – 2) Q(– 2) + (– 2 + 2) = ((– 2)2– (– 2) – 2) (3) + (0) = 12
*** P(x) dibagi (x2+ 3x + 2) adalah
P(x) = (x2+ 3x + 2) R(x) + ax + b
P(– 2) = (x2+ 3x + 2) R(– 2) + a(– 2) + b = – 2a + b = 12 ...............................................................1)
P(– 1) = (x2+ 3x + 2) R(– 1) + a(– 1) + b = – a + b = 1 ....................................................................2)
1) dan 2) dieliminasi sehingga diperoleh a = – 11 dan b = – 10 maka sisanya adalah – 11x – 10
-
17
21
29
38
42
Jawaban : d* Karena kurva melalui titik (1, 15), maka
(1,15)→y=ax2+bx+c
15=a+b+c…..(1)
** Kurva tegak lurus dengan garis x + 7y = 0 → m1 = -1/7, maka gradien garis yang tegak lurus m2=7
y'=2ax+b
m2=f'(1)
7=2a+b….(2)
*** a, b, c membentuk barisan aritmatika berarti a+c=2b…..(3)
**** Subtitusikan persamaan (3) ke persamaan (1) didapat :
2b+b=15
3b=15
b=5…..(4)
***** Subtitusiikan (4) ke (2) didapat a=1….(5)
Subtitusikan (5) dan (4) ke (1) didapat 15=1+5+c
c=9
a+2b+3c=1+2(5)+3(9)=38
-
1
4
Jawaban : c
-
Misalkan f(1) = 2, f’(1) = –1, g(1) = 0 dan g’(1) = 1. Jika F(x) = f(x) cos (g(x)), maka F’(1) = ...
2
1
0
-1
-2
Jawaban : dF(x) = f(x) cos (g(x))
F’(1) = ...
F’(1) = f’(1) cos (g(1) – sin (g(1)) . g’(1) . f(1)
F’(1) = (–1)(1) – 0 (1)(2) = –1
-
Diberikan sistem persamaan :
x + y2 = y3
y + x2 = x3
Banyaknya pasangan bilangan real (x, y) yang memenuhi sistem di atas adalah ....
0
1
2
3
tak hingga
Jawaban : dPersamaan x + y2 = y3 merupakan persamaan y + x2 = x3 yang dicerminkan terhadap garis y = x, sehingga pasangan bilangan real yang memenuhi terletak pada garis y = x.
Akibatnya diperoleh:
x + x2 = x3 ⇒ x + x2 – x3 = 0
⇒ x(1 + x – x2) = 0
Diperoleh x = 0 merupakan salah satu solusi, dan karena 1 + x – x2 mempunyai determinan 5 maka 1 + x + x2 mempunyai 2 solusi berlainan. Jadi totalnya ada 3 buah solusi, sehingga ada 3 pasangan bilangan real yang memenuhi sistem persamaan yang dimaksud.
-
Jika x, y, z masing-masing bilangan bulat yang memenuhi 27x – 28y + 29z = A dan 2x + 2z = 40 + 2y dengan y – 2z < 0 dan 2x > y, maka bilangan asli A yang memenuhi adalah ....
510 < A < 520
540 < A < 580
560 < A < 580
580 < A < 600
600 < A < 620
Jawaban : by – 2z < 0 dan 2x > y
–y + 2z > 0 dan –2x + y < 0,
dan karena
2x + 2z = 40 + 2y
maka
x – y + z = 20
⇒ 27x – 27y + 27z = 540
⇒ A = 540 – y + 2z > 540
29x – 29y + 29z = 580
⇒ A = 580 – 2x + y < 580
Akibatnya 540 < A < 580.
-
Jika suku banyak f(x)+g(x) dibagi x2–2x+1 bersisa 2x–1 dan jika xf(x)+g(x/3) dibagi x2–3x bersisa x+2, maka f(1)+g(1)+g(0) = ....
0
1
2
3
4
Jawaban : dMisal h(x) = f(x) + xg(x), maka
h(1) = f(1) + 1g(1)
= 2(1) – 1 ⇒ f(1) + g(1) = 1
Misal j(x) = xf(x) + g(x/3),
maka j(0) = 0f(0) + g(x/3)
= 0 + 2 ⇒ g(0) = 2
Jadi f(1) + g(1) + g(1) + g(0) = 3
Bagian 2
-
Banyak parabola Ax2 + Cy = 0 dengan A dan C dua bilangan berbeda yang dipilih dari {0, 1, 4, 16} adalah ….
10
8
6
4
3
Jawaban : cSyarat parabola: A ≠ 0 dan C ≠ 0
maka:
(3) (2) = 6
-
Jumlah akar-akar persamaan |x|2 - 2|x| - 3 = 0 sama dengan….
-10
-3
-1
0
4
Jawaban : d -
Diketahui fungsi-fungsi f dan g dengan f(x) g(x) = x2 - 3x untuk setiap bilangan real x. Jika g(1) = 2, dan f’(1) = f(1) = -1, maka g’(1)….
2
1
0
-1
-3
Jawaban : d -
Diketahui x1 dan x2 merupakan akar-akar persamamaan x2 + 5x + a = 0 dengan x1 dan x2 kedua-duanya tidak sama dengan nol. x1, 2x2, dan -3x1x2 masing-masing merupakan suku pertama, suku kedua, dan suku ketiga dari deret geometri dengan rasio positif, maka nilai a sama dengan…..
-6
2
6
-6 atau 6
2 atau 3
Jawaban : c -
Luas daerah yang dibatasi oleh y=2 sin x, x=π/2, x=3π/2, dan sumbu x sama dengan……
1 satuan luas
2 satuan luas
3 satuan luas
4 satuan luas
5 satuan luas
Jawaban : d -
Satuan limas beraturan T.PQRS dengan TP = TQ = TR = TS = √21 cm dan PQRS adalah suatu persegi dengan panjang sisi 6 cm. Besar sudut antarbidang TQR dan bidang alas sama dengan….
30o
45o
60o
75o
90o
Jawaban : a -
Untuk 0 ≤ x ≤ 12, maka nilai x yang memenuhi pertidaksamaan
adalah .....
0 ≤ x ≤ 3 atau 6 ≤ x ≤ 9
0 ≤ x ≤ 3 atau 6 ≤ x ≤ 12
2 ≤ x ≤ 4 atau 8 ≤ x ≤ 10
1 ≤ x ≤ 3 atau 9 ≤ x ≤ 11
0 ≤ x ≤ 2 atau 10 ≤ x ≤ 12
Jawaban : e -
Jika x = a, y = b, dan z = c adalah penyelesaian dari sistem persamaan linear:
x + y = 3
x + z = 4
y + z = 5maka nilai a2 + b2 + c2 sama dengan ....
6
9
11
14
19
Jawaban : d -
Jika f(2x+4) = x dan g(3-x) = x, maka nilai f(g(1)) + g(f(2)) sama dengan ....
2
3
4
5
6
Jawaban : b -
Diketahui matriks
dan
.
Bilangan λ yang memenuhi [A − λΙ] = 0 adalah ....
-1 atau 0
1 atau 3
-1 atau 2
2 atau 3
-1 atau 3
Jawaban : c
Bagian 3
-
x3 - x2 + 5x + 1
x3 - x2 + 2x + 4
x3 - x2 + 4x + 2
x3 - x2 + x + 5
x3 - x2 + 3x + 3
Jawaban : e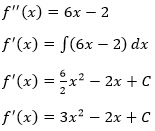
garis singgung y = f(x) di titik A(1,6) mempunyai gradien 4, berarti f' (1) = 4

Grafik y = f(x) melalui titik A(1,6), berarti f(1) = 6
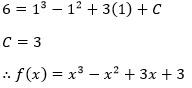
-
1/9√3
1/9√2
1/6√3
1/6√2
1/3√2
Jawaban : ePerhatikan gambar berikut.

Perhatikan segitiga ABC

Berdasarkan aturan pada segitiga samasisi AT' = 2/3 AP
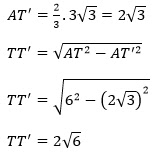
Kemudian berdasarkan prinsip kesebangunan
PP' = ½ . 2√6 =
Perhatikan segitiga APP'

-
 Jawaban : e
Jawaban : e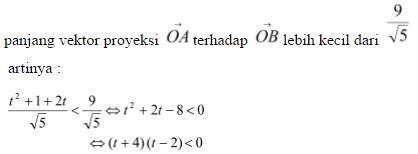
Sehingga:
-4 < t < 2
-
Jawaban : a
* P(x) = (x2– x – 2) Q(x) + (x + 2) maka
P(2) = (x2– x – 2) Q(2) + (2 + 2) = 4
P(– 1) = (x2– x – 2) Q(– 1) + (– 1 + 2) = 1
** Q(x) dibagi (x + 2) mempunyai sisa 3 maka Q(–2) = 3
P(– 2) = ((– 2)2– (– 2) – 2) Q(– 2) + (– 2 + 2) = ((– 2)2– (– 2) – 2) (3) + (0) = 12
*** P(x) dibagi (x2+ 3x + 2) adalah
P(x) = (x2+ 3x + 2) R(x) + ax + b
P(– 2) = (x2+ 3x + 2) R(– 2) + a(– 2) + b = – 2a + b = 12 ...............................................................1)
P(– 1) = (x2+ 3x + 2) R(– 1) + a(– 1) + b = – a + b = 1 ....................................................................2)
1) dan 2) dieliminasi sehingga diperoleh a = – 11 dan b = – 10 maka sisanya adalah – 11x – 10
-
17
21
29
38
42
Jawaban : d* Karena kurva melalui titik (1, 15), maka
(1,15)→y=ax2+bx+c
15=a+b+c…..(1)
** Kurva tegak lurus dengan garis x + 7y = 0 → m1 = -1/7, maka gradien garis yang tegak lurus m2=7
y'=2ax+b
m2=f'(1)
7=2a+b….(2)
*** a, b, c membentuk barisan aritmatika berarti a+c=2b…..(3)
**** Subtitusikan persamaan (3) ke persamaan (1) didapat :
2b+b=15
3b=15
b=5…..(4)
***** Subtitusiikan (4) ke (2) didapat a=1….(5)
Subtitusikan (5) dan (4) ke (1) didapat 15=1+5+c
c=9
a+2b+3c=1+2(5)+3(9)=38
-
1
4
Jawaban : c
-
Misalkan f(1) = 2, f’(1) = –1, g(1) = 0 dan g’(1) = 1. Jika F(x) = f(x) cos (g(x)), maka F’(1) = ...
2
1
0
-1
-2
Jawaban : dF(x) = f(x) cos (g(x))
F’(1) = ...
F’(1) = f’(1) cos (g(1) – sin (g(1)) . g’(1) . f(1)
F’(1) = (–1)(1) – 0 (1)(2) = –1
-
Diberikan sistem persamaan :
x + y2 = y3
y + x2 = x3
Banyaknya pasangan bilangan real (x, y) yang memenuhi sistem di atas adalah ....
0
1
2
3
tak hingga
Jawaban : dPersamaan x + y2 = y3 merupakan persamaan y + x2 = x3 yang dicerminkan terhadap garis y = x, sehingga pasangan bilangan real yang memenuhi terletak pada garis y = x.
Akibatnya diperoleh:
x + x2 = x3 ⇒ x + x2 – x3 = 0
⇒ x(1 + x – x2) = 0
Diperoleh x = 0 merupakan salah satu solusi, dan karena 1 + x – x2 mempunyai determinan 5 maka 1 + x + x2 mempunyai 2 solusi berlainan. Jadi totalnya ada 3 buah solusi, sehingga ada 3 pasangan bilangan real yang memenuhi sistem persamaan yang dimaksud.
-
Jika x, y, z masing-masing bilangan bulat yang memenuhi 27x – 28y + 29z = A dan 2x + 2z = 40 + 2y dengan y – 2z < 0 dan 2x > y, maka bilangan asli A yang memenuhi adalah ....
510 < A < 520
540 < A < 580
560 < A < 580
580 < A < 600
600 < A < 620
Jawaban : by – 2z < 0 dan 2x > y
–y + 2z > 0 dan –2x + y < 0,
dan karena
2x + 2z = 40 + 2y
maka
x – y + z = 20
⇒ 27x – 27y + 27z = 540
⇒ A = 540 – y + 2z > 540
29x – 29y + 29z = 580
⇒ A = 580 – 2x + y < 580
Akibatnya 540 < A < 580.
-
Jika suku banyak f(x)+g(x) dibagi x2–2x+1 bersisa 2x–1 dan jika xf(x)+g(x/3) dibagi x2–3x bersisa x+2, maka f(1)+g(1)+g(0) = ....
0
1
2
3
4
Jawaban : dMisal h(x) = f(x) + xg(x), maka
h(1) = f(1) + 1g(1)
= 2(1) – 1 ⇒ f(1) + g(1) = 1
Misal j(x) = xf(x) + g(x/3),
maka j(0) = 0f(0) + g(x/3)
= 0 + 2 ⇒ g(0) = 2
Jadi f(1) + g(1) + g(1) + g(0) = 3
1 2 3











